



|
Tweet
Pin
It
|
Sets, Relations and Functions :
Sets and their representation; Union, intersection and complement of sets
and their algebraic properties; Power set; Relation, Types of relations,
equivalence relations, functions;. one-one, into and onto functions, composition
of functions.
Complex Numbers and Quadratic Equations :
Complex numbers as ordered pairs of reals, Representation of complex
numbers in the form a+ib and their representation in a plane, Argand diagram,
algebra of complex numbers, modulus and argument (or amplitude) of a complex
number, square root of a complex number, triangle inequality, Quadratic
equations in real and complex number system and their solutions. Relation
between roots and co-efficients, nature of roots, formation of quadratic
equations with given roots.
Matrices and Determinants :
Matrices, algebra of matrices, types of matrices, determinants and matrices
of order two and three. Properties of determinants, evaluation of determinants,
area of triangles using determinants. Adjoint and evaluation of inverse
of a square matrix using determinants and elementary transformations,
Test of consistency and solution of simultaneous linear equations in two
or three variables using determinants and matrices.
Permutations and Combinations :
Fundamental principle of counting, permutation as an arrangement and combination
as selection, Meaning of P (n,r) and C (n,r), simple applications.
Mathematical Induction :
Principle of Mathematical Induction and its simple applications.
Binomial Theorem and its Simple Applications :
Binomial theorem for a positive integral index, general term and middle
term, properties of Binomial coefficients and simple applications.
Sequences and Series :
Arithmetic and Geometric progressions, insertion of arithmetic, geometric
means between two given numbers. Relation between A.M. and G.M. Sum upto
n terms of special series: Sn, Sn2, Sn3. Arithmetico - Geometric progression.
Limit, Continuity and Differentiability :
Real - valued functions, algebra of functions, polynomials, rational,
trigonometric, logarithmic and exponential functions, inverse functions.
Graphs of simple functions. Limits, continuity and differentiability.
Differentiation of the sum, difference, product and quotient of two functions.
Differentiation of trigonometric, inverse trigonometric, logarithmic,
exponential, composite and implicit functions; derivatives of order upto
two. Rolle’s and Lagrange’s Mean Value Theorems. Applications
of derivatives: Rate of change of quantities, monotonic - increasing and
decreasing functions, Maxima and minima of functions of one variable,
tangents and normals.
Integral Calculus :
Integral as an anti - derivative. Fundamental integrals involving algebraic,
trigonometric, exponential and logarithmic functions. Integration by substitution,
by parts and by partial fractions. Integration using trigonometric identities.
Evaluation of simple integrals of the type
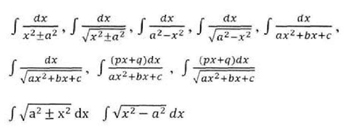
Integral as limit of a sum. Fundamental Theorem of Calculus. Properties
of definite integrals. Evaluation of definite integrals, determining areas
of the regions bounded by simple curves in standard form.
Differential Equations :
Ordinary differential equations, their order and degree. Formation of
differential equations. Solution of differential equations by the method
of separation of variables, solution of homogeneous and linear differential
equations of the type:
dy/dx + p (x) y = q (x)
Co-Ordinate Geometry :
Cartesian system of rectangular co-ordinates in a plane, distance formula,
section formula, locus and its equation, translation of axes, slope of
a line, parallel and perpendicular lines, intercepts of a line on the
coordinate axes.
Straight lines
Various forms of equations of a line, intersection of lines, angles between
two lines, conditions for concurrence of three lines, distance of a point
from a line, equations of internal and external bisectors of angles between
two lines, coordinates of centroid, orthocentre and circumcentre of a
triangle, equation of family of lines passing through the point of intersection
of two lines.
Circles, conic sections
Standard form of equation of a circle, general form of the equation of
a circle, its radius and centre, equation of a circle when the end points
of a diameter are given, points of intersection of a line and a circle
with the centre at the origin and condition for a line to be tangent to
a circle, equation of the tangent. Sections of cones, equations of conic
sections (parabola, ellipse and hyperbola) in standard forms, condition
for y = mx + c to be a tangent and point (s) of tangency.
Three dimensional Geometry :
Coordinates of a point in space, distance between two points, section
formula, direction ratios and direction cosines, angle between two intersecting
lines. Skew lines, the shortest distance between them and its equation.
Equations of a line and a plane in different forms, intersection of a
line and a plane, coplanar lines.
Vector Algebra :
Vectors and scalars, addition of vectors, components of a vector in two
dimensions and three dimensional space, scalar and vector products, scalar
and vector triple product.
Statistics and Probability :
Measures of Dispersion
Calculation of mean, median, mode of grouped and ungrouped data. Calculation
of standard deviation, variance and mean deviation for grouped and ungrouped
data.
Probability
Probability of an event, addition and multiplication theorems of probability,
Baye’s theorem, probability distribution of a random variate, Bernoulli
trials and Binomial distribution.
Trigonometry :
Trigonometrical identities and equations. Trigonometrical functions. Inverse
trigonometrical functions and their properties. Heights and Distances.
Mathematical Reasoning :
Statements, logical operations and, or, implies, implied by, if and only
if. Understanding of tautology, contradiction, converse and contrapositive.
Find it Useful ? Help Others by Sharing Online
Comments and Discussions |
Related
Entrance Exams
|
|||
|
|